My research is in the field of low-dimensional topology, particularly knot theory. Knot theory is a mathematical discipline that began in the late nineteenth century as the study of smooth embeddings of the circle into . In the intervening period, knot theory has expanded into a much broader field which encompasses the study of a variety of knot-like objects using techniques from many other mathematical disciplines. Within mathematics, knot theory has been connected to the general topological study of manifolds via surgery, as well as representation theory and—more broadly—category theory. Outside of mathematics, knot theory has been related to quantum physics and, more recently, to biology (particularly regarding protein and DNA structure). My research is focused on the study of quantum invariants and homological theories of knots and links.

My dissertation work focussed on the functoriality of odd Khovanov homology.  I am currently working with my advisor Stephan Wehrli to extend and publish three sections of my dissertation work. The first is in preprint, we are projecting two more papers.

My other major research has been in the area of shadow diagrams for links embedded in lens spaces , and analogs of classical knot theory invariants for lens space knots arising through these diagrams.

Preprints:

• Functoriality of Odd and Generalized Khovanov Homology in
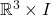
  • With Stephan Wehrli arxiv: 2410.23455

Projected Papers:

• A module structure on odd Khovanov homology and the odd invariant for ribbon 2-knots
  • With Stephan Wehrli
• An action of the Hecke algebra H(−1, n) on the odd Khovanov homology of certain cables
  • With Stephan Wehrli

For more detailed information about my recent and planned research please look at my up-to-date Research Statement.